New Paper: Phase Distribution Graphs
In this paper (https://onlinelibrary.wiley.com/doi/full/10.1002/mrm.30055) Jonathan Endres and Co-Authors present an analytical Bloch simulation approach for arbitrary MRI sequence simulation called Phase Distribution Graphs. It is a general implementation of the Extended Phase Graph (EPG) concept, based on the Fourier-domain Bloch equation, but with arbitrary timing, and including the exact contribution of dephased states resulting from spatial encoding and T2’ relaxation effects. In contrast to EPG, which was limited to echo amplitudes only, this allows calculation of full echo shapes. The Pytorch implementation provides full differentiability in all input parameters allowing gradient descent optimization. A major problem of phase graphs, the generation of an „astronomical number of states“ is solved by an efficient state selection algorithm. The simulation compares well to results of conventional Bloch simulations with quasi-random isochromat distribution, which it outperformed in simulation time by at least one order of magnitude. Different sequences and their artifacts are analyzed and improved, underlining that Phase Distribution Graphs allow efficient simulation and optimization of arbitrary MRI sequences, which was previously only possible via high isochromat counts.
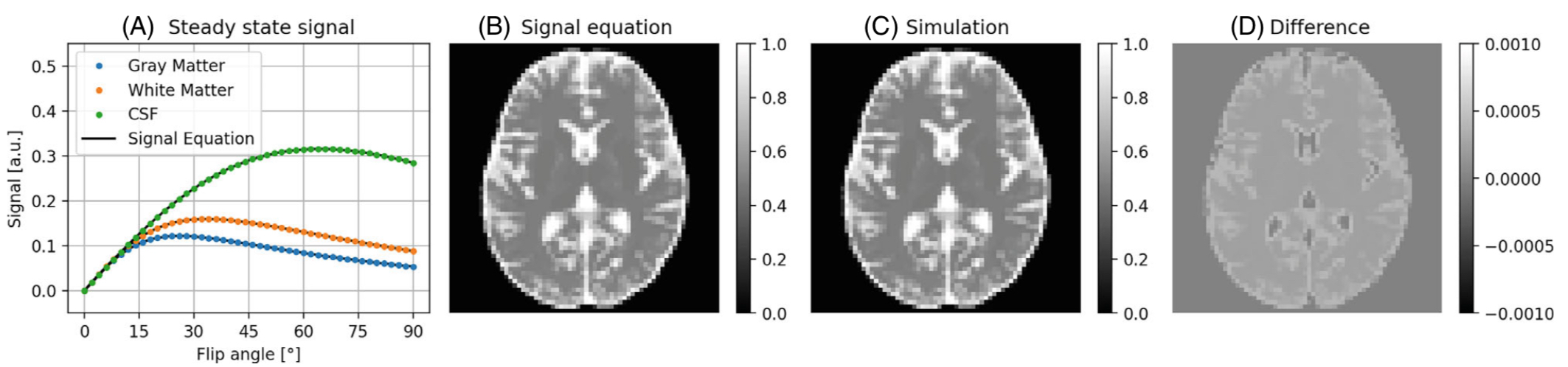
Figure 1: The PDG simulation matches an analytical solution of the steady-state bSSFP.
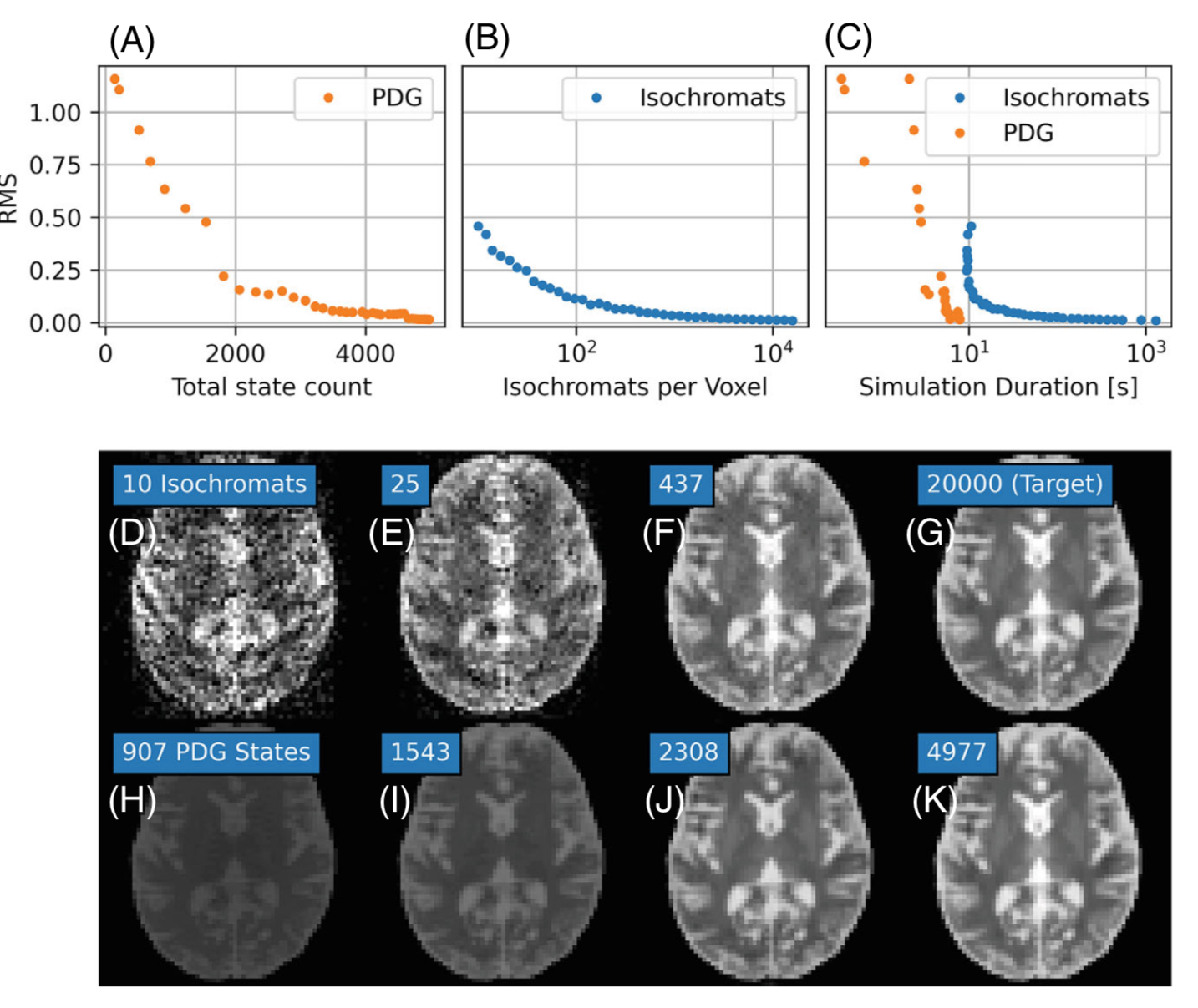
Figure 2: PDG converges faster than isochromat solutions. In many sequences simulation is more than an order of magnitude faster.
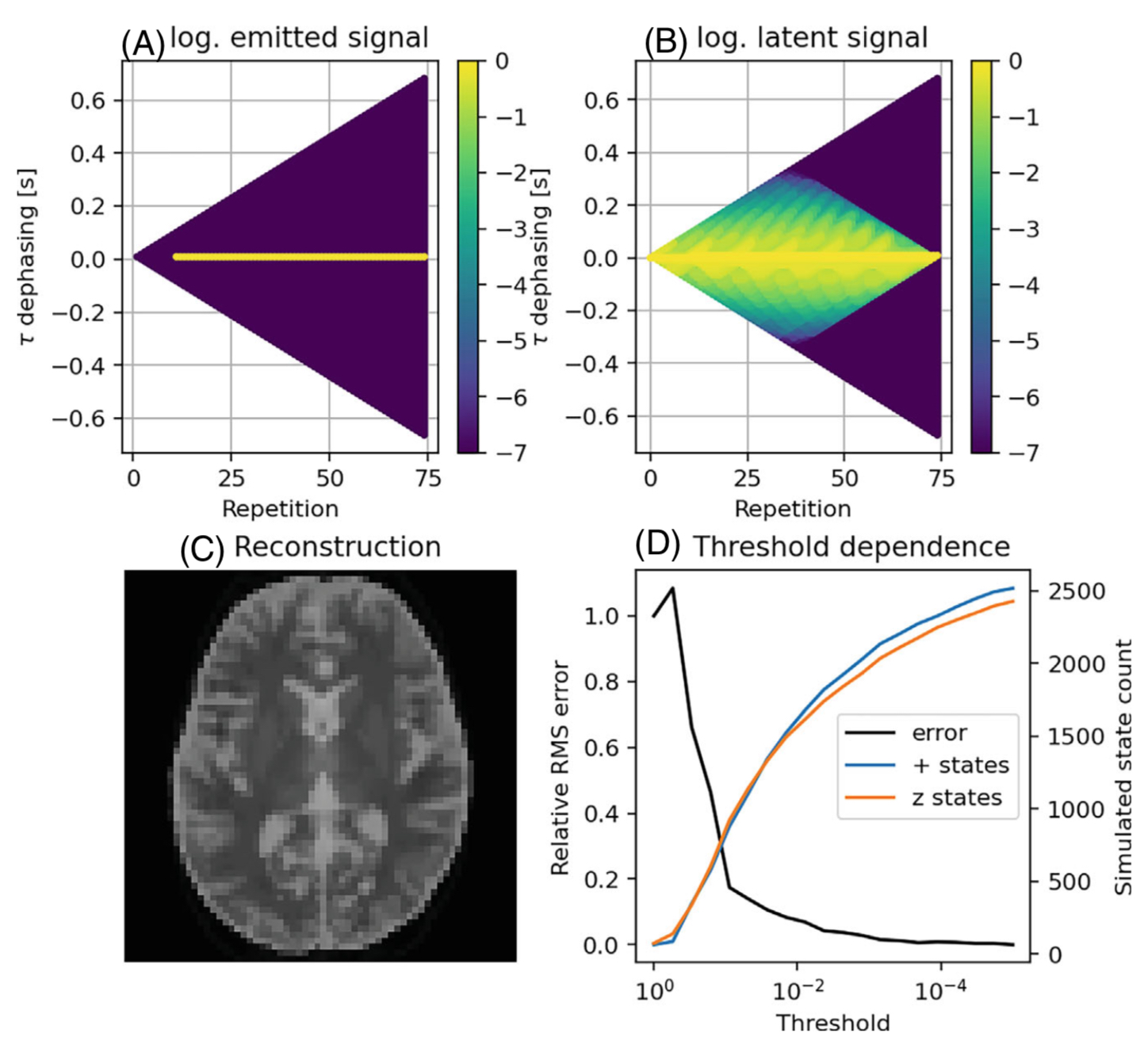
Figure 3: PDG provides deep insight into the contributing echo paths to each signal via the newly introduced latent signal.
